Los humanos parecemos tener una compulsión, innata o que se estabiliza en los primeros años de vida, tendente a percibir todo (y a describir todo lo que percibimos) en forma secuencial (temporal), espacial, y causal (en cadenas de causa-efecto) (véase v.g. https://entenderelmundo.com/2018/05/11/la-sintesis-kantiana-entre-racionalismo-y-empirismo/; https://entenderelmundo.com/2018/05/14/schopenhauer-el-mundo-como-voluntad-y-representacion/; https://entenderelmundo.com/2018/04/25/las-metaforas-y-la-construccion-imaginaria-de-la-realidad/). Somos sistemas complejos sometidos a un proceso permanente de cambio, y que construye representaciones sobre lo que es el mundo, a partir de percepciones muy puntuales procedentes de éste. Esto no significa que cualquier representación que podamos crear tenga la misma validez práctica. Dentro de nuestros pre-condicionamientos constitutivos a la hora de construir representaciones, no todas las descripciones espacio-temporales y causales que podemos hacer de la realidad se ajustan a lo que observamos de forma consistente y coherente, es decir, de forma pragmáticamente útil a la hora de manipular y de predecir el comportamiento futuro de los objetos observados. El llamado “conocimiento científico” no es sino el estado actual de esa pragmática en la que un conjunto de metáforas y conceptos sobre supuestos objetos reales (y clases de objetos) ha sido aceptado como el conjunto cuya coherencia y consistencia intrínseca (de unos conceptos observacionales con los otros) es máxima.
Las descripciones científicas de la realidad se hacen utilizando modelos, que son conjuntos muy especiales de metáforas y conceptos. Un modelo contiene un conjunto de teorías generales sobre la clase de objetos a la que supuestamente pertenece el objeto descrito y también un conjunto de hipótesis auxiliares sobre características únicas del objeto que estamos describiendo y el ambiente que le rodea. Normalmente, los modelos científicos se construyen en forma matemática.
En las “instrucciones de uso” de un modelo también hay que definir la «escala espacio-temporal» en la que se debería observar la realidad para poderla comparar con lo que el modelo predice (o escala espacio-temporal de aplicabilidad del modelo) y la definición de lo que debería considerarse como “las variables de interés” del objeto observado. No todas las propiedades observables en el objeto las consideramos importantes y relevantes para el modelo; sólo algunas de ellas. El conjunto elegido constituye el «sistema de interés». Esta elección de variables y escala del “observador-modelador” tendrá pues un importante efecto sobre los resultados y predicciones que se obtendrán del modelo.
Hay algunos casos en los que la relación particular entre »observador-modelador» y »objeto observado-modelado» puede ser olvidada sin que los resultados del modelo pierdan validez. Son aquellas en las que existe un acuerdo previo e incontrovertido entre las diversas partes interesadas que utilizarán el modelo, sobre cómo interaccionarán con el objeto, sobre la ‘‘escala espacio-temporal’’ a la que interesa observarlo (por ejemplo, los distintos ambientes, momentos y geografías en los que los actores observarán al objeto real no lo afectarán hasta el punto de convertirlo en otra cosa a una velocidad que requeriría un análisis evolutivo complementario) y hay también un consenso previo sobre lo que debería considerarse como «el sistema de interés», dentro de la variedad de detalles diferentes con los que se puede presentar una misma clase de objetos en momentos y sitios diferentes y para observadores diferentes.
En los apartados que siguen resumiremos la forma como la ciencia actual ha llegado a concebir los procesos de cambio en los objetos más complejos que percibe y describe, y analizaremos con más detalle el ejemplo concreto de la biosfera.
Sistemas disipativos y sistemas auto-organizativos
Todos los sistemas naturales de interés para la sostenibilidad y para la supervivencia de los humanos sobre el planeta Tierra (por ejemplo, los ciclos biogeoquímicos complejos, las células vivas que realizan la fotosíntesis, los sistemas ecológicos, o los sistemas humanos cuando se analizan en diferentes niveles de organización y escalas por encima de la molecular) son “sistemas disipativos”. Esto es, son sistemas atravesados por flujos de energía, lejos del equilibrio termodinámico, y afectados por procesos auto-organizativos.
Ejemplos de procesos auto-organizativos relativamente simples son los cilindros de agua rotante (o las columnas hexagonales) que se forman en una caja con agua calentada por debajo; o las ondas y espirales que se producen en las reacciones químicas no-lineales, como la de Belusov-Zhabotinski, y que a veces siguen una pauta periódica y otras se generan de forma caótica e impredecible.
Resumamos las características de los procesos auto-organizativos. (i) Se dan en sistemas alejados del equilibrio y abiertos a la energía y/o a los materiales externos, por lo que no son sistemas hamiltonianos (que conservan su energía total) sino sistemas abiertos disipativos (que toman energía de baja entropía del medio, la hacen circular entre sus componentes, y la dejan salir de nuevo al medio con mayor entropía de la que entró).
(ii) Muestran creación espontánea (no buscada por el observador humano) de inhomogeneidad y cambios cualitativos donde su estado previo era homogéneo y/o estable.
(iii) Sus variables observables a escala macroscópica (como la temperatura o la densidad) interactúan de un modo no-lineal. En los modelos matemáticos de los sistemas de este tipo, cuando hay más de dos variables (y una variable que varía espacialmente, como las de un fluido, equivale a infinitas variables) el sistema puede generar atractores para la evolución de sus variables, esto es, trayectorias recurrentes hacia las que las variables del sistema tienden. Los atractores pueden ser estacionarios, ciclos limite, ciclos multiples, o atractores caóticos.
Desde el punto de vista del modelo matemático, la estructura disipativa se produce cuando el sistema, que estaba inicialmente en un estado estacionario (típico en muchos sistemas termodinámicos abiertos), (a) pierde la estabilidad y (b) cae en otro atractor de igual o mayor complejidad.
¿Cómo se produce la inestabilización del sistema? Prigogine distingue tres formas: (a) por la aparición de una fluctuación suficientemente intensa de las componentes, que desestabiliza el atractor actual de la dinámica macroscópica del sistema; (b) por cambio en los parámetros externos que controlan los flujos, fuerzas termodinámicas, interacciones entre las partículas o probabilidades de interacción entre los subsistemas («inestabilidades sinergéticas» sistematizadas posteriormente por H. Haken), o (c) por inestabilidad estructural ante la aparición de nuevos componentes y/o nuevas interacciones («inestabilidad estructural ante la aparición de nuevas variables»).
La primera clase de inestabilidad es muy improbable en sistemas con atractores intensos que llevan funcionando establemente mucho tiempo, porque esto mismo es una demostración de que son estables ante las fluctuaciones estadísticas habituales en sus componentes y en el entorno; pero todo sistema compuesto de partes es sólo “metaestable”, esperando el tiempo suficiente es siempre posible que aparezca una fluctuación estadística que meta en el sistema una concentración de energía anómala del entorno, o que lleve una gran parte de la energía del sistema hacia un grupo de componentes que, al moverse sincronizadamente, pueden romper la (meta)estabilidad del sistema.
En las inestabilidades de tipo (b) (sinergéticas), los parámetros del medio ambiente dentro del cual está el sistema pueden ir modificándose lentamente a lo largo de periodos de tiempo mucho más dilatados que los tiempos típicos de cambio del propio sistema; ello puede acabar volviendo inestable a los atractores que ordenan el comportamiento del sistema. Éste puede volverse inestable porque se modifiquen las tasas de interacción con el entorno, las restricciones externas, o las probabilidades de interacción entre sus subsistemas componentes (por ejemplo, partículas). Esto último genera una posibilidad adicional de comportamiento complejo, pues tales probabilidades de interacción pueden estar siendo modificadas por alguna de las emergencias macroscópicas generadas por la interacción de los componentes.
La aparición de columnas de convección de forma hexagonal en sistemas naturales o de laboratorio se pueden predecir mediante esta clase de modelos sinergéticos.

Columnas de convección formadas espontáneamente en un lago salino
La reacción de Belousov-Zhabotinsky es otro ejemplo. El atractor estacionario del sistema se ha debilitado por variación de sus parámetros, y pequeñas perturbaciones locales producidas por la propia turbulencia del fluido, por una vibración sonora, o por la acumulación casual de muchas moléculas de ácido malónico en un mismo punto, pueden desencadenar la amplificación de una pauta macroscópica, que en cada momento es diferente, como muestra la figura siguiente.

Las inestabilidades del tercer tipo son importantes cuando estructuras previamente autoorganizadas y que tienen cierta (meta)estabilidad se encuentran unas con otras y alguna propiedad emergente de una afecta a la dinámica de la otra. La aparición de simbiosis o endosimbiosis entre células simples puede modelarse en principio mediante esta clase de inestabilización de estructuras previas que se encuentran por azar.

Las células eucariotas parecen haber surgido de la entrada simbiótica de células procariotas dentro del citoplasma de otra célula procariota receptora
Aún no se ha podido encontrar una ley universal válida para la evolución de cualquier sistema alejado del equilibrio. Lo más que se puede hacer es construir el diagrama de bifurcaciones e inestabilidades para las clases de sistema cuya forma de inestabilizarse tiene una estructura matemática recurrente. Al hacerlo, conviene tener en cuenta que: (i) el sistema puede contener impurezas e influencias no consideradas al escribir las ecuaciones, que proceden de escalas inferiores (escala “micro”) a la de observación (escala “macro”); (ii) no siempre se puede aislar el sistema de la aparición de nuevos elementos y/o interacciones a nivel microscópico (a escala de los constituyentes); (iii) hay que considerar, además, las fluctuaciones de las variables macro relevantes (originadas muchas veces en la impredecibilidad de comportamiento de los componentes), su probabilidad, y su influencia en la trayectoria del sistema por su “espacio de fases” (conjunto de valores accesibles a sus variables macro v1,v2…vn). Por ello, la predicción de los modelos suele dar la probabilidad P(v; t) de que en el tiempo futuro t el estado del sistema sea v= (v1,v2…vn). Si no hubiera fluctuaciones, P sería siempre una distribución de varianza nula o «delta de Dirac» (trayectoria determinista); debido a la existencia de fluctuaciones y perturbaciones impredecibles, y la forma como las interacciones internas del sistema reaccionan ante ellas, las variables vi se distribuyen con cierta probabilidad en torno a una trayectoria media en muchos sistemas naturales. Las fluctuaciones y su forma estadística se convierten en determinantes en momentos en que un atractor se convierte en inestable o se bifurca. Por ello, en tales momentos las descripciones macro y mesoscópica se vuelven insuficientes, y se suele recurrir al uso de ecuaciones, llamadas «master», para la evolución de la probabilidad P.
Finalmente, hay un tema de reflexión muy interesante, y es el de cuál es el rasgo común que tiene el proceso de inestabilización del estado estacionario en sistemas tan distintos como una reacción química y un fluido por ejemplo, y por qué tal estado nunca se vuelve inestable cuando el sistema está “cerca del equilibrio” (atravesado por flujos débiles de energía). ¿En qué consiste esa retroalimentación positiva o catálisis entre componentes micro que desestabiliza el estado estacionario y genera una pauta macro nueva? Una respuesta heurística a esta cuestión podría ser la siguiente:
En los sistemas cerca del equilibrio, las fluctuaciones no son lo suficientemente intensas como para provocar encuentros lo suficientemente frecuentes entre los elementos micro.
Por contra, si hay mayor densidad de energía, materiales y momento atravesando al sistema, en forma de fuertes flujos y fuerzas termodinámicas (que aumentan las energías internas y/o potenciales), habrá mayor energía disponible para fluctuaciones grandes (y pequeñas).
Por otro lado, los encuentros entre los constituyentes (colisiones si son partículas) generan propiedades emergentes que (i) son posibilitadas por los encuentros y (ii) muchas veces se intensifican con la frecuencia de encuentros. Y tales propiedades emergentes facilitan (probabilísticamente) la continuación del tipo de encuentros que es capaz de producirlas (en un verdadero «embuclamiento» micro→macro→micro). En esto parece consistir en general la autocatálisis, que es el rasgo principal de la auto-organización.
Muchas veces, la autocatálisis producto de las colisiones (o los encuentros, o las interacciones entre componentes) basta para generar emergencias como las correlaciones a largas distancias de las propiedades macroscópicas generadas por esas sincronizaciones micro.
Es importante resaltar que la metodología reduccionista utilizada por la ciencia mecanicista hasta bien entrado el siglo XX presupone que explicar el comportamiento o las propiedades del todo a partir de sus partes es “objetivo” mientras que explicar el comportamiento de las partes a partir del todo, eso no es objetivo ni científico. Sin embargo, la retroacción de la propiedad emergente macroscópica sobre el comportamiento (o las propiedades) de los constituyentes es algo que aparece una y otra vez en procesos complejos; y esta evidencia es devastadora para las pretensiones del reduccionismo (Rosen, 1993). La aplicabilidad de éste debe ser circunscrita en lo sucesivo a situaciones muy particulares del objeto y de los sujetos que lo describen.
Sistemas que se auto-mantienen
Los sistemas que se automantienen son sistemas constituidos por sistemas auto-organizativos cuyos atractores (estacionarios o cíclicos) mantienen a sus variables macro emergentes en cierta (meta)estabilidad. De este modo, los sistemas auto-organizativos componentes pueden permitirse mantener cierta persistencia en la interacción de sus propiedades (variables) emergentes con las de otros componentes. Pero además, y este es el rasgo esencial de los sistemas que se automantienen, los sistemas componentes se producen unos a los otros de forma operacionalmente cerrada (Hejl 1984). Esto es, los materiales y energía requeridos por cada componente proceden de los materiales y energía liberados por otros componentes. Para resaltar y modelar la materialidad de esos flujos en red entre los ingredientes de un ensamblaje que se automantiene, el concepto de red o hiperciclo de auto-mantenimiento puede ser de gran utilidad. Se trata de un esquema de flujos materiales (y energéticos) entre los componentes del sistema, tal como el de la Figura siguiente.

Los sistemas que se auto-mantienen son la consecuencia de un bucle de retroalimentación constructivo (organización) que permite la regeneración continua de los componentes (Varela 1974).
Los lazos causales y materiales cerrados que son característicos de los sistemas que se auto-mantienen impiden la posibilidad de explicar de forma reduccionista (a partir de las propiedades de las partes únicamente) el comportamiento de tales sistemas (Rosen 1993).
Sistemas auto-poiéticos
Los sistemas auto-poiéticos se pueden considerar casos especialmente complejos de sistemas que se auto-mantienen. Un sistema autopoietico se organiza (definido como una unidad) como una red de procesos de producción (transformación y destrucción) de componentes que producen los componentes que:
- a través de sus interacciones y transformaciones, continuamente regeneran y realizan la red de procesos (relaciones) que los produjeron; y
- Lo constituyen [a la red que se auto-mantiene] como una unidad concreta en el espacio en el que [los componentes] existen especificando el dominio topológico de su realización como tal red (Varela 1979).
Un sistema autopoiético es siempre un sistema que se auto-mantiene. Pero la característica clave de un sistema autopoiético es el mantenimiento de su organización, es decir, la preservación de la red relacional que lo define como una unidad sistémica. Esta invariancia o persistencia organizacional es el resultado crítico de la ‘autopoiesis’, mientras que la (re)producción de los componentes es el medio por el cual esto se lleva a término de forma continuada. De ahí la definición resumida de autopoiesis que Maturana (1975) ha empleado a veces: «Los sistemas autopoiéticos operan como sistemas homeostáticos que tienen su propia organización como la variable crítica fundamental que ellos activamente mantienen constante”.
Los sistemas auto-poiéticos son además sistemas autónomos, esto es, sistemas organizacionalmente cerrados que no son dependientes de procesos de control externos a su organización (o hiperciclo de flujos). Según Varela, si a un sistema autopoiético se le quita la propiedad de que las componentes están siendo producidas físicamente por la organización de los flujos, entonces nos queda un sistema autónomo. El concepto de sistema autónomo y el de sistema que se auto-mantiene son vecinos. Si aceptamos nuestra definición, un sistema que se auto-mantiene sería un sistema autónomo (organizacionalmente cerrado) cuyas componentes son sistemas auto-organizativos. Por otra parte, una sociedad sería un sistema autónomo, dado que sus componentes son sistemas autopoiéticos humanos (que son sistemas autoorganizativos), artefactos (que no son sistemas autoorganizativos) y sistemas socio-técnicos institucionalizados (una combinación de los dos anteriores).
Un ejemplo de sistemas autopoiéticos son los organismos procariotas. Una célula viva es un caso especial de sistema auto-poiético en el que sus componentes son moléculas orgánicas. La figura siguiente esquematiza los principales flujos moleculares entre enzimas (proteínas catalizadoras) componentes de una célula. La red completa es un hiperciclo que representa al metabolismo celular.

Esquema de los flujos principales del metabolismo celular. El círculo central es el ciclo de Krebs
Todo ese hiperciclo cerrado de flujos materiales exige la vecindad de los materiales reactantes y de las enzimas catalizadoras de las reacciones. Esta vecindad es posibilitada por la presencia de una membrana celular cerrada que impide la libre difusión de los materiales por el espacio.
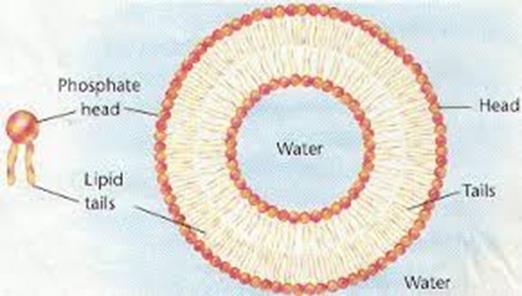
Las moléculas de fosfolípidos tienen la propiedad de que, cuando son agitadas por la turbulencia en un medio acuoso, orientan espontáneamente sus cabezas hidrofílicas hacia las moléculas de agua y sus colas hidrofóbicas lejos del agua. Esto les permite formar estructuras bicapa como la de la figura. Este parece ser el origen de las membranas biológicas, una estructura auto-organizada sobre la que la selección natural pudo actuar, añadiendo mecanismos metabólicos reparadores, canales y otras sofisticaciones. Aunque son estables, tales membranas pueden sufrir accidentes y, en esos casos, una parte del metabolismo de la célula procariota se activa y se encarga de su reparación. Dentro de esa estructura pudo evolucionar un metabolismo celular auto-poiético que añadió innovaciones a la propia membrana, como la aparición de canales con puertas que pueden sea abiertas o cerradas por moléculas específicas, lo cual permitió la comunicación de la célula con el medio exterior y con otras células.
Sistemas auto-referenciales y otros
Mingers (1997) y otros autores han diferenciado otras clases de sistemas complejos, pero no necesariamente auto-poiéticos, que establecen relaciones circulares de algún tipo. Los más relevantes son los siguientes:
Sistemas que se auto-influyen: Sistemas dinámicos que tienen bucles causales o causalidad circular (retroalimentaciones positivas o negativas). Ejemplo: Tamaño y tasa de crecimiento de una población.
Sistemas que se auto-regulan: Sistemas que mantienen alguna variable en un nivel particular (homeostasis). Ej.: El sistema de regulación de la temperatura corporal.
Sistemas organizacionalmente cerrados: Sistemas en que sus componentes y procesos son dependientes unos de otros para el funcionamiento del conjunto y de sí mismos, pero que no necesariamente producen sus propias componentes.
Sistemas que se auto-reconocen: Sistemas capaces de reconocer sus propios componentes (y eventualmente rechazar componentes no «propios») pero que, de nuevo, pueden necesitar de otros sistemas externos para su propio mantenimiento. Ej.: Sistema inmunológico.
Sistemas que se auto-replican: sistemas que construyen réplicas de ellos mismos. Ej.: Virus, bacterias, organismos que se reproducen.
Varela también distinguió los sistemas auto-referenciales. Son sistemas que organizan los estados de sus sistemas componentes de un modo operacionalmente cerrado. Pero no necesariamente son sistemas auto-poiéticos, pues sus componentes pueden no estar siendo producidos por el propio sistema, sino por sistemas exteriores. Son sistemas similares a los que Mingers (1997) llama “autorreferentes” y que serían sistemas simbólicos o representativos que se refieren a sí mismos ya sea por alguna forma de señalar a la propia organización como una unidad; o por contener una imagen de sí mismos dentro de sí mismos; o porque se refieren a ellos mismos lingüísticamente. El cerebro podría ser un sistema auto-referencial.
Sistemas que se auto-conocen: Sistemas que generan identidad cognitiva. Ej.: animales con sistemas nerviosos que interaccionan simbólicamente.
Sistemas auto-conscientes: Sistemas capaces de interaccionar con descripciones de ellos mismos (el observador observando al observador). Ej.: Una persona diciendo “actué egoístamente hoy”.
Sistemas jerárquicos
Un sistema que se auto-mantiene es habitualmente un sistema jerárquico. O’Neill (1989) define sistema jerárquico de este modo: “un sistema disipativo es jerárquico cuando opera en múltiples escalas espacio-temporales, esto es, cuando se encuentran en el sistema diferentes tasas de procesamiento”. Otra definición útil que da de los sistemas jerárquicos es: «los sistemas son jerárquicos cuando son analizables en conjuntos sucesivos de subsistemas».
La existencia de diferentes niveles y escalas en las que opera un sistema jerárquico implica la inevitable existencia de formas no equivalentes de describirlo. Por ejemplo, podemos describir a un ser humano en el nivel microscópico para estudiar el proceso de digestión de nutrientes dentro de su cuerpo. Sin embargo, este tipo de descripción no sería compatible con la descripción que se requeriría para describir su «cara» a otro ser humano (Giampietro 2005).
Los seres vivos, las sociedades humanas y los ecosistemas son generados por procesos que operan en varios niveles jerárquicos sobre una cascada de diferentes escalas. Por lo tanto, son ejemplos perfectos de sistemas jerárquicos disipativos anidados que requieren una pluralidad de descripciones no equivalentes para ser utilizadas en paralelo para analizar sus características relevantes en relación con la sostenibilidad.
Sistemas complejos adaptativos
Los componentes de un sistema complejo pueden ser autómatas. Un autómata es cualquier elemento que puede interaccionar con su entorno, tiene un código interno (o programa) para interpretar esas interacciones y modificar su estado interno acorde con ellas, y produce una respuesta de acuerdo con el cambio de su estado interno. Cuando el autómata tiene sensores y programas sofisticados de respuesta se suelen denominar agente (v.g. un programa complejo de control de procesos, un robot, un ser humano). La respuesta de los autómatas y agentes puede ser determinista (una respuesta única, función de su estado interno actual) o estocástica (muchas respuestas posibles para un estado interno, que pueden obedecer, o no, a una distribución estable de probabilidad. A veces se habla de que un agente tiene un comportamiento “en parte determinista, en parte estocástico”. Esto significa que responde estocásticamente, pero que podemos predecir cómo evoluciona en el tiempo la distribución de probabilidad de sus respuestas.

Comportamiento del “Juego de la Vida” de Conway. Se trata de un sistema de autómatas estáticos en el cual cada autómata muere o sigue viviendo según una regla muy sencilla función del número de autómatas que lo rodeen, de los ocho vecinos posibles. Si esta regla se modificara en función de la historia pasada del autómata, el sistema se convertiría en adaptativo. De https://gliderlabs.com/devlog/2015/a-pattern-emerges/
Un sistema complejo adaptativo es un sistema: (i) compuesto de autómatas (o agentes) con un comportamiento en parte determinista y en parte estocástico; (ii) la respuesta (o comportamiento futuro) determinado de cada agente es una función determinista de su estado interno, el cual depende de las interacciones pasadas; (iii) la función determinista de respuesta (o comportamiento determinista) está controlada por un conjunto de reglas (o leyes) de interacción; (iv) cada agente modifica sus reglas (o leyes) de interacción en función de los resultados obtenidos por su comportamiento pasado.
Nótese que el punto (iv) supone implícitamente capacidades auto-referenciales en el agente, esto es, la capacidad de que una parte del agente sea sensible al estado del propio agente. El agente debe ser capaz, pues, de identificar su estado interno (efecto de su comportamiento e interacciones pasadas), asignarle un valor a este estado, y cambiar sus reglas de interacción en función de ese valor. Por supuesto, esta reflexividad no tiene por qué ser necesariamente consciente; la consciencia humana de uno mismo es una forma especial de reflexividad. Los agentes pueden interaccionar sólo localmente, con sus vecinos próximos, o simultáneamente con todos los agentes constituyentes del colectivo. Esta clase de modelos se han aplicado para representar interacciones entre humanos (modelados como agentes) sometidos a distintas reglas morales, o a distintas estrategias inversoras en un mercado, o a distintas preferencias políticas, etc. También se ha usado para modelar la creación de memes o pautas de opinión en redes de contactos o redes sociales de Internet. Otro campo de aplicación fructífero es la teoría de juegos evolutiva (que trata de identificar estrategias evolutivamente estables) y la toma de decisiones colectivas.
Las ciencias de la complejidad han seguido su curso desde sus inicios en la cibernética y la teoría de sistemas. La figura siguiente resume dicha evolución entre los años 50 y la actualidad.

La biosfera y la hipótesis Gaia
Bertalanffy (1952 pp. 124-125) fue uno de los primeros en caracterizar los seres vivos como estructuras que se autoproducen y automantienen canalizando por su interior un flujo continuo de energía y materiales que lo atraviesan:
Cuando comparamos objetos inanimados y animados encontramos un contraste sorprendente. Un cristal, por ejemplo, está construido de componentes invariables; persiste con ellos tal vez durante millones de años. Un organismo vivo, sin embargo, sólo en apariencia es persistente e invariable; en realidad es la manifestación de un flujo perpetuo. Como resultado de su metabolismo, que es característico de todo organismo vivo, sus componentes no son las mismas de un momento al siguiente. Las formas vivas no están en el ser, están sucediendo; ellos son la expresión de una corriente perpetua de materia y energía que atraviesa el organismo y al mismo tiempo lo constituye…
Esta concepción dinámica del organismo puede ser contada entre los principios más importantes de la biología moderna. Conduce a los problemas fundamentales de la vida, y nos permite explorarlos.
Desde el punto de vista de la física, el estado característico en que encontramos el organismo vivo se puede definir afirmando que no es un sistema cerrado con respecto a su entorno, sino un sistema abierto que continuamente entrega materia al mundo exterior e incorpora materia de él, pero que se mantiene a sí mismo en este intercambio continuo en un estado estacionario, o se aproxima a ese estado estacionario en sus variaciones en el tiempo.
En su libro The evolution of the biosphere (1986) M. I. Budyko usó el término “biosfera” para designar el Sistema constituido por todas las especies vivas. Un hecho esencial de este sistema según Budyko es que las tasas de intercambio de materiales que se producen entre las especies son mucho más altas que las tasas de incorporación de estos materiales desde otros sistemas, como la litosfera, la hidrosfera o el espacio exterior. Además, estos intercambios de materiales sólo “se cierran” en la escala de la propia biosfera, no en escalas más locales como los ecosistemas particulares. Siguiendo esta perspectiva, podemos definir la biosfera como el sistema global de reciclado de los materiales que sirven como sustrato para el metabolismo y autopoiesis de los seres vivos. Barlow y Volk (1990) defienden una perspectiva similar a ésta sugerida por Budyko.
Lovelock y Margulis (1974) y Lovelock y Watson (1982) sugirieron que la biosfera controla la temperatura, la composición atmosférica y la disponibilidad de otros materiales que la vida utiliza como sustrato de su metabolismo, contribuyendo así a estabilizar las condiciones ambientales necesarias para su supervivencia. Esta es una hipótesis muy fuerte que ha suscitado un vivo debate desde entonces.
En su formulación fuerte, la hipótesis no parece sostenible. El sistema regulador principal que mantiene la temperatura del planeta aceptable para la vida es geológico: la meteorización de los silicatos del suelo por el ácido carbónico de la lluvia (procedente del CO2 tectónico) y su retroacción negativa: sobre la concentración atmosférica de CO2 tanto cuando ésta es alta como cuando la temperatura es alta (véase Historia del clima terrestre). El artículo de Kirschner (2003) ilustra otras críticas a esta formulación fuerte de la hipótesis Gaia. Tal como lo expone el resumen de dicho artículo: “Las incertidumbres que rodean el cambio climático global proporcionan amplia evidencia, si alguna fuera necesaria, de la necesidad de una visión sistémica de la Tierra. Podría decirse que el intento más visible, y controvertido, de entender la Tierra como un sistema ha sido la teoría Gaia de Lovelock. Gaia ha sido un generador de hipótesis fructíferas y ha generado muchas conjeturas interesantes sobre cómo los procesos biológicos podrían contribuir a la regulación a escala planetaria de la química atmosférica y el clima. En muchos casos importantes, sin embargo, estas conjeturas son refutadas por los datos disponibles. Por ejemplo, la teoría de Gaia predice que la composición de la atmósfera debería estar estrechamente regulada por los procesos biológicos, pero las tasas de absorción de carbono en la biosfera se han acelerado en solo un 2% en respuesta al aumento del 35% en el CO2 atmosférico desde los tiempos preindustriales. La teoría de Gaia predeciría que el CO2 atmosférico debería estar más efectivamente regulado por la captación del ecosistema terrestre (que está mediada biológicamente) que por la captación oceánica (que es principalmente abiótica), pero ambos procesos son igualmente insensibles a los niveles de CO2 en la atmósfera. La teoría de Gaia predice que las retroalimentaciones biológicas deberían hacer al sistema Tierra menos sensible a la perturbación, pero los mejores datos disponibles sugieren que el efecto neto de las retroalimentaciones biológicamente mediadas será amplificar, no reducir, la sensibilidad del sistema terrestre al cambio climático antropogénico. La teoría de Gaia predice que los subproductos biológicos en la atmósfera deberían actuar como reguladores del clima planetario, pero el núcleo de hielo de Vostok indica que el CO2, el CH4 y el sulfuro de dimetilo, todos subproductos biológicos, funcionan calentando la Tierra cuando hace calor; y enfriándola cuando hace frío. La teoría de Gaia predice que las retroalimentaciones biológicas deberían regular el clima de la Tierra a largo plazo, pero los picos en la paleo-temperatura se corresponden con los picos en el paleo-CO2 en registros que se remontan al Pérmico; por lo tanto, si el CO2 está regulado biológicamente como parte de un termostato global, ese termostato ha estado conectado al revés durante al menos los últimos 300 millones de años. La teoría de Gaia predice que los organismos alteran su medio ambiente para su propio beneficio, pero en la mayor parte de la superficie del océano (que comprende más de la mitad del globo), el agotamiento de nutrientes por el plancton casi ha creado un desierto biológico, y se mantiene bajo control solo por la hambruna de nutrientes del propio plancton. Por último, cuando los organismos mejoran su entorno por sí mismos, crean una retroalimentación positiva; por lo tanto, los dos principios centrales de la teoría de Gaia: primero, que los organismos estabilizan su entorno, y segundo, que los organismos alteran su entorno de manera que los beneficia, son mutuamente inconsistentes entre sí. Estos ejemplos sugieren que el desarrollo posterior de la teoría de Gaia requerirá una comparación más ajustada de la teoría y los datos.”
En efecto, el aumento de CO2 atmosférico tiende a aumentar el CO2 disuelto en el océano, lo cual tiende a aumentar la propducción primaria (fotosintética) en los océanos y con ello la tasa de producción de esqueletos carbonatados que caen hacia el fondo (tras la muerte de los animales con concha o esqueleto calcáreo). Pero este efecto es compensado con creces por dos retroalimentaciones que actúan en sentido contrario y que son provocadas por la vegetación de los continentes. El primero es el siguiente: cuando sube el CO2 atmosférico, la vegetación continental se vuelve más densa; esto fija el terreno y disminuye la resuspensión de polvo (que es rico en hierro) por el viento; la disminución del hierro que llega a los océanos disminuye la producción neta de éstos; esto tiende a aumentar el CO2 en atmósfera, lo cual aumenta la temperatura; tanto el aumento de CO2 como de temperatura tienden a aumentar la densidad de la vegetación. El segundo es el siguiente: cuando sube el CO2, la vegetación se vuelve más densa; esto disminuye el albedo de los continentes; esto aumenta la temperatura de los continentes; el aumento térmico aumenta la densidad de vegetación que cubre las regiones frías, lo cual disminuye aún más el albedo. Como discute Bender (2003) ambas retroalimentaciones positivas tienen un efecto mayor que el del CO2 sobre la tasa biológica de sedimentación de carbonatos marinos, de modo que el efecto neto es que, cuando la concentración de CO2 aumenta en la atmósfera, la vegetación planetaria tiende a aumentar aún más esa concentración de CO2, un efecto desestabilizador y no estabilizador sobre el clima, al contrario de lo esperable según la hipótesis Gaia.
Barlow y Volk utilizan el término Gaia y no el de biosfera, no en el sentido fuerte que le da Lovelock, sino como forma de subrayar que esta biosfera es una entidad global que es probablemente más autónoma, más autorregulada y más persistente que sus ecosistemas constituyentes o los agregados de ecosistemas. Podemos llamar a esto el planteamiento débil de la hipótesis Gaia.
Estos autores sugieren que la naturaleza casi cerrada del sistema tierra para los flujos de materiales impuso una presión de selección a todas las especies desde el principio. Esta presión tendió a seleccionar las combinaciones de especies que tenían mayores capacidades de reciclar (conjuntamente) materiales esenciales.
Para ello se apoyan en Margulis y Sagan, quienes describen la secuencia de eventos en la evolución de los procariotas como habiendo sido provocada por una escasez tras otra. Las primeras formas de vida pueden haberse alimentado de productos químicos libremente disponibles y de ATP generado abióticamente. La evolución de la fermentación simple liberó a la vida de los límites impuestos por la cantidad de ATP generado abióticamente, porque los azúcares generados abióticamente podían ahora consumirse para generar ATP. A la escasez de azúcar le siguió la evolución de nuevas formas de fermentación por las cuales las bacterias podrían derivar energía de los desechos metabólicos (ácidos y alcoholes) de otros fermentadores. Otras bacterias desarrollaron estrategias metabólicas por las cuales el ATP era construido desde sulfatos. Luego se produjo la evolución de diferentes estrategias fotosintéticas que usaban la energía del sol para construir carbohidratos a partir del último producto de desecho, el dióxido de carbono, y alguna fuente de hidrógeno. La disponibilidad de gas hidrógeno y de sulfuro de hidrógeno de origen volcánico (y de los residuos metabólicos de bacterias del azufre) puso un límite a la cantidad de actividad fotosintética que podía inicialmente ser soportada. Pero cuando una bacteria mutante fue capaz de extraer el hidrógeno nada menos que rompiendo la estable molécula de agua, tuvo lugar un salto cuantitativo para la biomasa terrestre. Como lo expresaron Margulis y Sagan, la inexorable pérdida de hidrógeno que sufre un planeta interior de baja gravedad “condujo a una de las mayores innovaciones evolutivas de todos los tiempos: el uso del agua en la fotosíntesis. Pero también condujo a una tremenda crisis de contaminación, la acumulación de gas oxígeno, que era originalmente tóxico para la gran mayoría de los organismos».
Entonces, aprovechando la nueva oportunidad – oxígeno libremente disponible – los organismos procariotas evolucionaron incorporando otra serie de estrategias metabólicas: respiración con oxígeno del hidrógeno fermentable para formar agua, de metano para formar dióxido de carbono, del sulfuro para formar sulfito, y del amoniaco para formar nitrato. Otro efecto que tuvo la rotura de la molécula de agua por los organismos fotosintetizadores y la presencia de oxígeno en la atmósfera fue la oxidación de la mayoría del hierro disuelto y ligado a las rocas de los océanos, lo que convirtió a este metal en un factor limitante del crecimiento de los organismos marinos.
Barlow y Volk citan también la evolución de las técnicas de captura de nitrógeno como otro ejemplo del papel que tuvo el cierre planetario a los materiales en la evolución de la vida. Los procesos abióticos originales fueron la oxidación del nitrógeno atmosférico por los rayos, que produjeron NO, NO2 y NO3, y la fotolisis del amoniaco que producía nitrógeno atmosférico. A estos procesos originales, la vida añadió sucesivamente el consumo de amoníaco, la amonificación o producción de NH3, la asimilación de nitratos, la nitrificación (o producción de NO2 y NO3 a partir de NH3), y la fijación de nitrógeno (o producción de NH3 a partir de N2 atmosférico). La escasez de nitrógeno fácilmente disponible y la demanda biológica de fuentes adicionales parecen haber sido las fuerzas motrices en tales innovaciones evolutivas.
Diversidad biológica y resiliencia
En ecología, la resiliencia se define como la capacidad de un ecosistema de mantener las mismas relaciones entre sus poblaciones después de sufrir perturbaciones externas; esto es, la magnitud de la perturbación que un ecosistema puede soportar antes de cambiar su estructura (Holling, 1973). Sin embargo, el concepto ha tomado un significado algo más amplio en estudios de sistemas socio-ecológicos. Por ejemplo, como subraya Castillo-Villanueva y Velázquez-Torres (2014), algunos autores plantean la resiliencia como la capacidad de un sistema de mantener sus funciones y estructuras básicas en momentos de choques y perturbaciones (Birkmann, 2006: 15-16). Otros señalan que “la resiliencia implica que el sistema, ya sea social, ecológico o socio-ecológico, puede movilizar la suficiente auto-organización para mantener las estructuras y los procesos esenciales mediante adaptación o estrategias de supervivencia. Otros definen la resiliencia como la capacidad de un sistema, comunidad o sociedad para anticiparse o adaptarse a los efectos de un evento peligroso, absorberlos o recuperarse de ellos, en forma oportuna y eficiente, garantizando la preservación, la restauración o la mejora de sus estructuras y funciones básicas y esenciales”. Esto es, se asume implícitamente que el sistema puede sufrir restructuraciones en sus componentes (e.g. especies) y en algunos de sus atractores emergentes, pero manteniendo las funciones principales (atractores emergentes principales).
Si definimos pues, qué retroalimentaciones y ciclos del hiperciclo de un sistema son los esenciales para garantizar sus funciones emergentes principales, todo sistema, ante una variable externa perturbadora, tiene un rango de resiliencia, un valor (con su incertidumbre asociada) para el cual la estructura esencial del sistema sufre un cambio irreversible, y un rango de vulnerabilidad, o rango de valores de la variable perturbadora para el cual el sistema no puede mantener su estructura anterior.
En ecología, hay bastante consenso en que la biosfera como un todo ha demostrado una enorme resiliencia ante cambios climáticos muy intensos (como se discute en Historia del clima terrestre); y que esta resiliencia está asociada a la gran diversidad de los ecosistemas terrestres. La diversidad biológica a su vez está relacionada con la abundancia de genes diferentes, de especies, y de hábitats.

Selva macrotérmica, con clima Af (sin época de sequía) en Barro Colorado (Panamá), que muestra la gran diversidad ecológica en este tipo de vegetación que tiene muchas especies con distintas épocas de floración. Los pájaros e insectos se encargan de la polinización, por lo que la diversidad existente es origen de su alimentación continua. Se puede ver la característica fundamental de la selva ecuatorial: miles de especies vegetales por unidad de superficie, pero pocos ejemplares de cada una, también por la misma unidad de superficie.
Stuart Kauffman ha estudiado cómo ha podido surgir y evolucionar esa gran biodiversidad utilizando modelos de sistemas complejos de agentes adaptativos. Consideremos el conjunto de todos los genes humanos, unos 80.000, cada uno de los cuales puede estar activo o inactivo, según sean activados o desactivados por la combinación de señales (traídas por proteínas) procedentes de otros genes con los que cada gen está conectado a distancia. El número de estados posible para una célula es de 280000, unos 1024000 estados. Si se tardara un segundo en activar o desactivar un gen, una célula tardaría 1024000 segundos en explorar todos sus posibles estados, esto es, unos 426 billones (1012) de años, necesitaría un tiempo muy superior al que lleva existiendo el universo (13.800 millones). Las células, sin embargo, no parecen explorar la totalidad de sus posibles estados de activación genética, sino más bien explorar ciclos concretos cerrados de activaciones que, tras varias horas, o días de tiempo, vuelven a un estado inicial.
Supongamos que una célula tiene solo tres genes, A, B y C, cada uno de los cuales puede estar activo (1) o inactivo (0). El conjunto de los 8 estados posibles sería: {(000),(001),(010),(011),(100),(101),(110),(111)}. En un sistema dinámico determinista, dado un estado del sistema en el tiempo t, el sistema cambia a otro estado sucesor que es único, y función del estado precedente; si el sistema no es determinista, cambia a uno de los N estados sucesores posibles de acuerdo con cierta distribución de probabilidad.
Supongamos que nuestro sistema de genes celulares es determinista. La función de cambio de estado podría ser la definida por la tabla siguiente:
T T+1
(ABC) (ABC)
(000) → (110)
(001) → (010)
(010) → (010)
(011) → (100)
(100) → (011)
(101) → (110)
(110) → (111)
(111) → (110)
Con tales reglas de transición entre estados, el sistema genera tres bucles finales, ciclos de estados, o “atractores” de tipo ciclo-límite, tal como se muestra en el esquema siguiente:
(101)
↓
(000) →(110) →(111) →(110)
(001) →(010) →(010)
(100) → (011) →(100)
El primer ciclo límite se produce entre los estados (110) y (111). El segundo ciclo se produce simplemente entre el estado (010) y él mismo, o sea, más que un ciclo límite se puede llamar un atractor estable. El tercer ciclo límite se produce entre (100) y (011). Estos ciclos finales pueden llamarse “atractores”, pues atraen hacia ellos el flujo de otros estados “transitorios”, como los estados ((101), (000), o (001). El conjunto de los estados que fluyen hacia un atractor más los estados que componen el propio atractor se llama “cuenca de atracción” del atractor. Las cuencas de atracción dividen el espacio de estados en conjuntos disjuntos.
Cuando el sistema tiene mucho más que tres genes y reglas de transición diferentes a esta, aparecen ciclos límites más largos, que relacionan cíclicamente a muchos genes a lo largo del tiempo. Kauffman y otros investigadores encontraron sistemáticamente tres formas de funcionamiento en estos sistemas de “genes” conectados: un régimen ordenado, un régimen caótico y un régimen fronterizo, o “frontera del caos”. En el régimen ordenado, la mayoría de los genes permanecen activados o desactivados la mayor parte del tiempo (generalmente dentro de un ciclo límite largo) y cambian su estado sólo de vez en cuando, y hay unos pocos grupos de genes que cambian de estado continuamente. En el régimen caótico, la situación se invierte: la mayoría de genes cambian de estado continuamente, mientras grupos aislados de genes permanecen estables o lentamente cambiantes. La frontera del caos es una situación intermedia entre los dos regímenes citados, y de transición entre los mismos.
En el régimen ordenado, las longitudes de los atractores crece de forma polinómica con el número de genes. En la frontera del caos, el número de estados de un ciclo es proporcional a la raíz cuadrada del número de genes. En el régimen caótico, la longitud de los ciclos crece exponencialmente con el número de genes.
Si, por ejemplo, la regla de transición cambia al azar en cada interacción, el resultado es un régimen caótico en el que la longitud típica de un ciclo de estados es de 212000 transiciones.
Dado que el ser humano tiene unos 80.000 genes, y la raíz de ese número es 283, si el genoma humano funcionara en un régimen ordenado pero cercano al caótico (o sea, en la vecindad o frontera del caos), debería tener ciclos de esa longitud. El número de clases de células humanas es d 256, por lo que Kauffman piensa que: (i) el sistema genético humano (con su citoplasma asociado) funciona en el régimen ordenado cercano al caos, (ii) los ciclos límite de activaciones del genoma humano corresponden a la construcción de todas las clases de células posibles para ese genoma; (iii) Además, el periodo de duración de un ciclo límite completo correspondería a los tiempos característicos de los ciclos biológicos: como lleva entre uno y diez minutos el activar o desactivar un gen eucariótico, el periodo de sus ciclos genéticos sería de entre 4.75 y 48 horas, un tiempo claramente en el margen de lo biológico.
Además, en el régimen ordenado pero fronterizo con el caos, el funcionamiento anómalo repentino de un gen se propaga perturbando solamente a un número de genes que es igual como máximo a dos veces la raíz cuadrada del número total de genes. En el régimen caótico, la avalancha afecta a casi la totalidad de los genes (el “efecto mariposa”, o sensibilidad exponencial a pequeñas diferencias iniciales, es la norma en los atractores caóticos). En la mosca Drossofila, que tiene unos 16.000 genes, la peor avalancha debería afectar a unos 254 genes; según Kauffman, la más grande observada hasta ahora afecta a unos 155 genes, luego el modelo resulta hasta el momento verosímil.
El mecanismo por el cual la evolución habría seleccionado a los organismos para que permanezcan en este régimen sería precisamente el que la diversidad genética hace más adaptable a una especie (al igual que hace más adaptable a un ecosistema). El régimen fronterizo con el caos es el que más eficazmente puede explorar las posibilidades genéticas posibles cercanas a las que están funcionando en un metabolismo celular dado; pero, lo hace sin que el metabolismo celular se vuelva super-crítico (caótico) y la célula empiece a tener un comportamiento molecularmente impredecible que sería incompatible con sus hiper-ciclos de auto-poiesis. Si alguna célula, alguna vez, ha traspasado esa frontera, con toda probabilidad se ha extinguido. Así que, según Kauffman, las especies y los ecosistemas tenderían a ser tan diversos como lo permite la dinámica de las relaciones entre agentes adaptativos en la frontera del caos.

La frontera del caos es un régimen de funcionamiento donde los comportamientos, y sus atractores, no son ni excesivamente predecibles ni absolutamente impredecibles, sino complejos.
Uno de los parámetros que la selección natural ha podido ir ajustando es el número K de entradas (señales de otros K genes) a las que cada gen es sensible. Kauffman, Derrida y Pomeau demostraron que si K=2 o inferior, las redes funcionan en el régimen ordenado, independientemente del contenido de las reglas de transición. Éstas pueden ser aleatorias, y aún así el funcionamiento es ordenado. Como dice Kauffman, “si tomamos 10.000 genes al azar y los combinamos también al azar con la única limitación de que tengan sólo K=2 entradas, aunque la función de transición asignada a cada gen sea aleatoria (de las 16 posibles), el sistema se las arregla para orbitar alrededor de sólo unos 100 estados de los 210000 posibles!”. Esta forma de autoorganizarse de los sistemas complejos de agentes, combinando cambios azarosos con atractores, sugiere que una parte importante del orden que observamos en los seres vivos procede de procesos autoorganizativos; y sobre ellos, actúa la selección natural perfilando los últimos detalles, por así decirlo.
Para valores de K mayores que 2, las redes funcionan en el régimen caótico, salvo si las funciones o reglas de transición poseen alguno de dos tipos de sesgo. El primer sesgo es que los genes tiendan a responder preferentemente con una clase de respuesta (i.e. activarse; o desactivarse) independientemente de la combinación de señales que reciba. Si la preferencia por una respuesta es del 80% de media, por ejemplo, los genes pueden tener 4 entradas y la red permanece en el régimen estable; si la preferencia es del 90%, pueden llegar a tener hasta 11 entradas, etc.
La segunda clase de sesgo (“reglas canalizadas”) es la de que la mayoría de los genes tienen alta sensibilidad (responden siempre) hacia las señales que reciben de algunos de los N genes, y baja sensibilidad (responden con poca frecuencia) hacia las señales que reciben de los demás genes. Kauffman encontró que los seres vivos utilizan esta segunda clase de sesgo sistemáticamente, para poder tener 4, 5 y 6 entradas por gen en algunos casos, y no utilizan la primera. Esto es, cada gen tiene “predilección” por lo que le señalan algunos genes concretos con los que está conectado, y reacciona más débilmente a los demás. Es plausible que la selección natural haya partido de redes autoorganizadas de genes con 2 conexiones por gen de media, y sobre ellas haya explorado el “entorno posible” de ese régimen añadiendo a la vez conexiones genéticas nuevas y reglas canalizadas (“preferencias” limitadas entre genes), manteniéndose así en el régimen fronterizo con el caos.
Este modelo ha sido utilizado por Kauffman también para simular de forma genérica el proceso de la co-evolución de dos especies. Considera una especie representada por un organismo típico con N genes, cada uno de ellos conectados a otros K genes. Todos los genes presentan dos versiones o «alelos» (0 y 1), y cada alelo de un gen hace una contribución distinta a la eficacia global del organismo; esa contribución depende de su propio alelo (0 o 1) y de los alelos (valores) de los K genes con los que está conectado. Habrá 2K+1 combinaciones de valores posibles, y cada una de ellas hace una contribución a la eficacia del organismo que Kauffman elige aleatoriamente (entro 0 o «mínima», y 1 o «máxima»).
La eficacia del organismo en un instante dado es definida, por ejemplo, como la media de las aportaciones hechas por cada uno de sus genes. Cuando K=0 en un sistema de este tipo, los N genes son independientes, hay un alelo óptimo para cada gen, y por tanto una eficacia del organismo óptima. Cualquier otra combinación de alelos (o «genotipo») tiene una eficacia inferior a la óptima, pero la selección natural puede ir aumentando su eficacia haciendo mutar sus genes uno por uno y seleccionando aquellas combinaciones que mejoran la eficacia. Cuando K=N-1, valor máximo posible, cada gen contribuye en la aportación a la eficacia de todos los demás; como esta aportación es aleatoria, el número de máximos locales para la eficacia es un número gigantesco: M = 2N/(N+1), y es prácticamente imposible encontrar el óptimo general por selección natural, el sistema siempre se quedará atrapado en algún pico local, y si tuviera algún mecanismo para saltar de vez en cuando de allí, aún así tardaría más tiempo que la edad del universo para encontrar el óptimo global entre esos M óptimos locales.
Kauffman estudia entonces la co-evolución de dos especies diferentes, una rana y una mosca por ejemplo. Cada uno de los N genes de la rana recibe entradas de K genes de la rana y de C genes de la mosca, y viceversa: una rana puede tener una lengua pegajosa, cuya eficacia se ve afectada por la presencia o ausencia de sustancias resbaladizas en el exoesqueleto de la mosca, por ejemplo. La selección natural que modifica el genoma de la rana hacia valores más altos modifica el relieve adaptativo de la mosca, cuya trayectoria ascendente por su propio relieve modifica a su vez el relieve adaptativo de la rana. Kauffman estudió sistemas co-evolutivos de 4, 8 y 16 especies y encontró que el ecosistema de 4 especies llega, tras algunas subidas y bajadas de las eficacias de todos los participantes, a un estado en el que las cuatro eficacias dejan de cambiar, un estado evolutivamente estable. Cada especie ha encontrado un óptimo local compatible con los óptimos locales propios encontrados por las otras especies. En ese estado, lo mejor que puede hacer cada especie es no cambiar mientras no lo hagan las demás. En cambio, en los ecosistemas de 8 o de 16 especies las eficacias suben y bajan siempre caóticamente a medida que las especies co-evolucionan. Sus propios óptimos adaptativos se desplazan más rápidamente de lo que ellas tardan en alcanzarlos, debido a las derivas genómicas de las demás especies. En las simulaciones de Kauffman, la K de cada especie puede ser modificada por selección natural si ello mejora la eficacia y, lo que se observa es que esa K tiende a aumentar en todas las especies pero que, cuando se hace demasiado alta, aumenta la frecuencia de grandes extinciones, por lo que los ecosistemas que sobreviven tienden a adoptar valores intermedios de K. Así pues en los ecosistemas, como en los organismos individuales, la evolución tiende a llevar al sistema a un régimen cercano a la frontera del caos, pero sin traspasar esa frontera (Kauffman, 1995; 2003).

Representación de las relaciones tróficas (o alimentarias, o de depredación) entre las especies de una comunidad biológica
El tamaño de los ecosistemas de especies en interacción también parece estar controlado espontáneamente por pautas autoorganizativas emergentes. Kauffman cita los trabajos de Stuart Pimm y Mack Post sobre comunidades arbitrarias de organismos autótrofos y heterótrofos. Las interacciones de tipo depredador-presa entre estos organismos se suelen representar mediante ecuaciones de Lotka-Volterra. Esencialmente, un organismo o bien es comido por otro(s), o bien come a otro(s) o ambas cosas a la vez, y las ecuaciones de Lotka-Volterra predicen el tamaño de la población de cada organismo en función del tiempo, cuando interacciona de ese modo con las otras poblaciones. Si solo hubiera una población de presas A y una población de depredadores B, las ecuaciones para las tasas de variación temporal de las poblaciones A y B serían:
dA/dt = p1 A – p2 AA – p3 AB
dB/dt = -p4 B + p5 AB
donde p1, p4 son parámetros que representan la tasa de crecimiento de ambas poblaciones en ausencia de depredación, p3, p5 son las tasas de crecimiento de ambas poblaciones debidas a los encuentros con la otra especie, y p2 es una tasa de frenado del crecimiento de la especie presa cuando su número se hace excesivo (impuesto por la capacidad de sustentación finita de los vegetales que come, o por la degradación del entorno que provoca la superpoblación, o por ambos factores).
Pimm y Post representaron en un modelo N especies cuyos parámetros p de interacción con otras eran tomados al azar. Entre los resultados posibles, estaba que todas las poblaciones se vinieran a cero (extinción de todas las especies), que sólo algunas poblaciones alcanzaran tamaños estables, que algunas de ellas oscilaran periódicamente y otras permanecieran estables, que todas subieran y bajaran caóticamente, etc. En contra de lo que esperaban, todas las poblaciones llegaron a un estado estacionario estable. Pimm y Post continuaron agregando especies al azar y observaron que, cuanto más especies había más difícil era añadir una nueva y que no se extinguiera (o extinguiera a otra al entrar ella en la relación). Sin embargo, la causa no era una falta de alimento o energía.
Según Bruce Sawhill y Tim Keitt, la situación que estamos considerando es equivalente a un problema lógico que se denomina Ksat. Tomemos una expresión lógica booleana. Toda expresión booleana puede ser traducida a su forma normal disyuntiva, esto es, cláusulas unidas por disyunciones («y»), por ejemplo: (A1 o A2) y (A3 o no A4) y (no A2 o no A3). Las expresiones entre paréntesis se llaman «cláusulas», en nuestro ejemplo tenemos tres cláusulas para cuatro variables (las «A»). La expresión lógica será cierta sólo si lo son todas las cláusulas. La primera cláusula será cierta sólo si A1 o A2 o ambas son ciertas; la segunda cláusula será cierta sólo si A3 es cierta o A4 es falso; la tercera será cierta sólo si A2 es falso o A3 es faso, o ambos lo son. Por todo ello, la expresión completa será verdadera, por ejemplo, cuando A1 = verdadero (o falso), A2 = verdadero, A3 = falso, A4 = falso. En cambio, hay expresiones para las cuales no hay ninguna combinación de valores para las variables que la hagan cierta. Por ejemplo, la expresión: (A2) y (no A2), que nunca es cierta, pues una cláusula contradice a la otra. En general, una expresión en su forma normal disyuntiva que contenga K variables en cada cláusula, un total de C cláusulas, y un total de V variables, puede ser satisfecha por muchas combinaciones distintas de valores de las variables; por sólo unas pocas combinaciones; o por ninguna combinación de valores. Lo curioso es que estos dos investigadores encontraron que para un número fijo V de variables y un número fijo K de variables en cada cláusula, si vamos aumentando el número de cláusulas C en una expresión arbitraria, al principio, hay muchas combinaciones que la satisfacen, y cerca del valor C/V = ln 2 · 2K el número de combinaciones cae exponencialmente a cero. Para ese valor crítico de C/V, la expresión (arbitraria) pasa de satisfacerse con casi total seguridad a no satisfacerse de ninguna manera.
Según estos autores, la formación de una comunidad trófica de criaturas elegidas al azar, con necesidades alimentarias y de interacción también aleatorias, es equivalente a un problema Ksat, puesto que encontraron la misma «transición crítica» en sistemas aleatorios de Lotka-Volterra que en el problema Ksat. La conclusión sería que, a medida que las comunidades tróficas aumentan en número de especies llega un momento en el que se cierran a cualquier intento de entrada de nuevas especies. Pero a largo plazo, si todas las especies de la red van aumentando en media el número de especies con las que interactúan (aumenta el número de especies «generalistas»), la red puede hacerse accesible de nuevo a especies adicionales.
Referencias
Barlow C. & Volk T. (1990). Open systems living in a closed biosphere: a new paradox for the Gaia debate. BioSysrems, 23, 371—384.
Bender M. 2003. Climate-biosphere interactions on glacial-interglacial timescales. Global Biogeochemical Cycles, Vol. 17, No. 3, 1082, doi:10.1029/2002GB001932
Bertalartffy, L.V., 1952, Problems of Life: An Evaluation of Modem Biological Thought, (John Wiley, New York).
Birkmann, Jörn, 2006: «Measuring vulnerability to promote disaster-resilience societes: conceptual frameworks and definitions», en Birkmann, Jörn. (Ed.): Measuring Vulnerability to Natural Hazards: towards disaster resilient societies, New Delhi, India: Teri Press.
Castillo-Villanueva L., Velázquez-Torres D. 2015. Sistemas complejos adaptativos, sistemas socio-ecológicos y resiliencia. Quivera, vol. 17, núm. 2, 2015
Hejl, P. M. (1984) Towards a Theory of Social Systems: Self-Organization and Self-Maintenance, Self-Reference and Syn-Reference, in Self-Organization and Management of Social Systems, H. Ulrich and G. J. B. Probst (eds.), Springer, Berlin.
Holling C. S. (1973). Resilience and Stability of Ecological Systems. Annual Review of Ecology and Systematics, Vol. 4, pp. 1-23.
Kauffman, S. (1995), At Home in the Universe, The Search for the Laws of Self-Organization and Complexity. Oxford University Press, New York.
Kauffman, S. (2003), Investigaciones, Barcelona,Tusquets.
Kirchner J. W. 2003. The Gaia Hypothesis: Conjectures And Refutations. Climatic Change 58: 21–45
Lovelock, J.E. and Margulis, L., 1974, Atmospheric homeostasis by and for the biosphere: the Gala hypothesis. Tellus 26, 1–9.
Lovelock, J.E. and Watson, A.J., 1982, The regulation of carbon dioxide and climate: Gaia or geochemistry, Planet. Space Sci. 30, 795–802.
Maturana, Humberto R. (1975). The organization of the living: A theory of the living organization, International Journal of Man-Machine Studies, Vol. 7, pp. 313-332.
Mingers J. 1997. Systems Typologies in the Light of Autopoiesis: A Reconceptualization of Boulding’s Hierarchy, and a Typology of Self-Referential Systems. SYST. RES. BEHAV. SCI. VOL. 14, 303-313.
O’Neill, R.V.: Perspectives in Hierarchy and Scale. In: J. Roughgarden, R.M. May and S. Levin (eds.): Perspectives in Ecological Theory. Princeton University Press, Princeton, 1989, pp. 140–156.
Rosen R. 1993. Drawing the boundary between subject and object: comments on the mind-brain problem. Theoretical Medicine 14.
Varela, Francisco J. (1979). Principles of Biological Autonomy, New York: Elsevier (North Holland).
Zhong Y.J., Huang K.K., Lan Y.F., Chen A.Q. 2018. Simulationof Carbon Isotope Excursion Events at the Permian-Triassic Boundary Based on GEOCARB. Open Geosci. 10: 441–451.
¡Muy buen artículo Antonio!, denso y sistemático como acostumbras. Aunque en mi caso me asaltan las dudas respecto a los intentos de reconstrucción de la «causalidad» que realiza la Ciencia actual, siento alejarme cada vez más de los intentos de reconstrucción que intenta la «dinámica» (¿mecánica?) de sistemas. Pero en cualquier caso me ha gustado mucho tu artículo
Un abrazo
David
Me gustaMe gusta
Gracias, David. ¿Para cuando tu próximo artículo en tu blog?
Me gustaMe gusta
Hola Antonio
He escrito 3 ya este año. Últimamente para mi es un récord y estoy redactando el 4º
Me gustaLe gusta a 1 persona